时间复杂度与空间复杂度

复杂度

  • 时间维度：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述。
  • 空间维度：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述

—What is Big O?—

O(1):Constant Complexity:Constant 常数复杂度 一次运算

O(log n):Logarithmic Complexity:对数复杂度

O(n):Linear Complexity: 线性时间复杂度（*） 循环n次

O(nlogn):线性对数阶

O(n^2):N square Complexity: 平方 时间复杂度是n^2

O(n^3):N square Complexity: 立方

O(n^k):k次方阶

O(2^n):Exponential Growth:指数

O(n！):Factorial 阶乘

注意：多块代码一起时，只看最高复杂度的运算

时间复杂度

image-20200402152728506

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
O(1):
int n=1000
system.out.println('print:'+n);

O(n)
    for(int i=1;i<=n;i++){
        system.out.println('print:'+i);
    }
O(n^2)
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
        system.out.println('print:'+i+'and'+j);
        }
    }
O(log n)//若n=4,则以下执行2次，而不是4次,即logn(底数为2)
     for(int i=1;i<=n;i=i*2){
        system.out.println('print:'+i);
    }
O(k^n)
    for(int i=1;i<=Math.pow(2,n);i++{//终止条件2^n
        system.out.println('print:'+i);
    }
O(n！)
    for(int i=1;i<=factorial(n);i++{
        system.out.println('print:'+i);
    }

log n 底数直接由分治的复杂度决定，采用二分法,那么就会以2为底数,三分法就会以3为底数，其他亦然。当n趋于无穷大时logx(n)/logy(n)的极限可以发现，极限等于lny/lnx（自然对数,底数为e，e=2.71828…），也就是一个常数，也就是说，在n趋于无穷大的时候，这两个东西仅差一个常数。所以从研究算法的角度log的底数不重要。

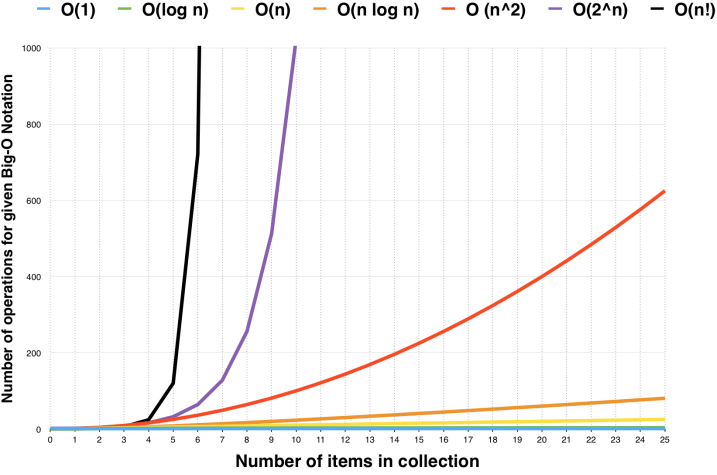
image-20200331102706328

横坐标：n 纵坐标：运行次数

常数、对数、线性、线性对数、平方、指数、阶乘

1
2
3
4
5
6
7
8
9
计算：1+2+3+...+n
y=0
for i=1 to n
    y=i+y
//硬循环,累加n次
求和公式：
    y=n*(n+1)/2
//只运行1次
时间复杂度由O(n)降为O(1)

用算法提高效率

斐波那锲数列（Fibonacci sequence）1、1、2、3、5、8、13、21、34…n

f(n)=f(n-1)+f(n-2)

1
2
3
4
5
6
7
8
9
10
递归
function fn(n){
    if(n==1|n==2){
        return 1;
    }
    return fn(n-1)+fn(n-2);
}
时间复杂度是2^n，或者说是O(k^n)
现实中n=6的话只需要计算6次，但计算机中算了不止6次，所以代码不是最优的
公司：Master Theorem（主定律）提供了用渐近符号表示许多由分治法得到的递推关系式的方法

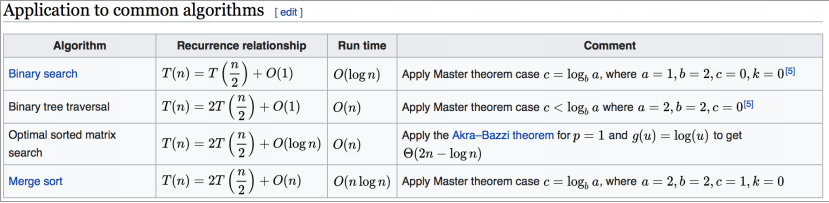
二分查找(Binary search)O(logn):一分为二，只查一边

二叉树遍历(Binary tree traversal):每个节点遍历一次且仅遍历一次O(n)

排序查找(Optimal sorted matrix serach):一维数组二分查找是O(logn）或排好序的二维矩阵的查找(O(n))

排序(Merge sort):（快排，归并排）O(nlogn)

image-20200331111710507

做自己不熟悉的算法题，比如常见的：动态规划，搜索，回溯，递归

https://leetcode.com/problemset/all/

中文社区：https://leetcode-cn.com/

切题：题目的范围、所有解法先思考一遍，找出最优的解法。

经常的面试题：二叉树遍历-前序、中序、后序：什么样子？时间复杂度是多少？

解题：时间复杂度为O(n),n代表二叉树的树的节点总数（通过主定理得到的）不论前序中序后序，它遍历二叉树时，每个节点会访问一次且仅访问一次，所以时间复杂度是线性于二叉树的节点总数，也就是O(n)的时间复杂度。

图的遍历：时间复杂度是多少？-》同理可得是O(n)，n代表图中节点总数

搜索算法：DFS（深度优先）、BFS（广度优先）时间复杂度是多少？-》同理可得是O(n)，n代表搜索空间里的节点总数

二分查找：时间复杂度是多少？-》logn

空间复杂度

与时间复杂度类似，但更加简单，主要两条原则：

1数组的长度：

例如一维数组，长度为传入元素的个数，一般来说空间复杂度就是O(n),如果是二维数组，数组的长度为n2,空间复杂度就是O(n2)

2递归的深度（特殊说明）

递归的深度就是空间复杂度的最大值，若递归中又开数组，那么两者之间的最大值就是你的空间复杂度。